Ki Wai Chau (CWI) - Fourier-based Expansion Approximation
December 19, 2018
In this informal talk, we consider numerical integration method based on series expansion and Fourier transform. Namely, we aim to approximate an expectation E[X] by a series in the form of \sum A_K V_k.
The talk will start with an introduction of the basic idea, followed by some insights from the research process.
The main goal of the talk is to provide a general picture on the derivation, extension and limitation of such method. The technical details will be kept at the minimal level (for all the people in holiday mood already).
Jonas Kremer (Bergische Universität Wuppertal) - On the long-time behavior of affine processes
December 13, 2018
In this talk we study stochastic stability properties of affine processes. An affine process with state space $\mathbb{R}_{\geq0}^m\times\mathbb{R}^n$, where $m,\thinspace n\in\mathbb{Z}_{\geq0}$ with $m+n>0$, is a time-homogeneous Markov process $(X_t)_{t\geq0}$ taking values in $\mathbb{R}_{\geq0}^m\times\mathbb{R}^n$, whose $\log$-characteristic function depends in an affine way on the initial value of the process, that is, there exist functions $\phi$ and $\psi=(\psi_1,\ldots,\psi_{m+n})$ such that
\[
\mathbb{E}\left.\left[\mathrm{e}^{\langle
u,X_t\rangle}\thinspace\right\vert\thinspace X_0=x\right]
= \exp\left(\phi(t,u)+\langle \psi(t,u),x\rangle\right),
\]
for all $u\in\mathrm{i}\mathbb{R}^{m+n}$, $t\geq0$, and $x\in\mathbb{R}_{\geq0}^m\times\mathbb{R}^n$. We provide sufficient conditions for the existence of limiting distribution of a conservative affine process. Our main theorem extends and unifies some known results for OU-type processes on $\mathbb{R}^{n}$ and one-dimensional CBI processes (with state space $\mathbb{R}_{\geqslant0}$). Finally, we present some results on the (exponential) ergodicity with respect to the Wasserstein distance and total-variation distance for interesting subclasses of affine processes.
Ziv Scully (CMU) - SOAP: One Clean Analysis of All Age-Based Scheduling Policies
December 10, 2018
We consider an extremely broad class of M/G/1 scheduling policies called SOAP: Schedule Ordered by Age-based Priority. The SOAP policies include almost all scheduling policies in the literature as well as an infinite number of variants which have never been analyzed, or maybe not even conceived. SOAP policies range from classic policies, like first-come, first-serve (FCFS), foreground-background (FB), class-based priority, and shortest remaining processing time (SRPT); to much more complicated scheduling rules, such as shortest expected remaining processing time (SERPT), the famously complex Gittins index policy, and other policies in which a job's priority changes arbitrarily with its age. While the response time of policies in the former category is well understood, policies in the latter category have resisted response time analysis. We present a universal analysis of all SOAP policies, deriving the mean and Laplace-Stieltjes transform of response time.
Guido Lagos (University of Santiago, Chile) - Systemic risk & reliability in networks: a new asymptotic analysis
December 05, 2018
Systemic risk in networks studies the risk of collapse of the entire system due to failure, shocks or actions of components of the network. This area has received particular attention in the last decade or so due to the need to better understand recent financial and economical crises. In this context, it is of interest to analyze, from a probabilistic perspective, the instant at which the whole system is considered to fail, in the case where there are failures that simultaneously affect several components of the network.
In this work we take a new approach in the field of reliability and systemic risk and study the following question: Are there asymptotical regimes for the probabilistic behavior of the network that allow to approximate the system and ultimately say something about the its reliability? Here, in broad terms, we refer to "asymptotic regime" as an equilibrium distribution or state of the system as the size of the network and time grow together in a "balanced" way. We answer the previous question in the positive, in the case where the dependency model for the failures is a particular exponential Marshall-Olkin copula and when the whole system is considered to fail when the last component fails — or more generally when the k-th component (out of a total of n components) fails.
Our main contribution is a collection of results giving a detailed analysis of a non-trivial scaling regime for the probability of the network being working at a certain time, as the time and size of the network scales. These approximations allow to estimate and give confidence bounds for the failure probabilities of the system. Moreover, the dependency model we study only needs to specify a reduced number of parameters, and our asymptotic results shed light on the effects of choosing such parameters.
Based on the paper https://arxiv.org/abs/1811.06034. Joint work with Javiera Barrera (Universidad Adolfo Ibáñez).
Guido's website: https://www2.isye.gatech.edu/~grlb3/
Yoav Kerner (Ben-Gurion University of the Negev) - Strategic behavior in an observable retrial queue
December 13, 2018
We consider a retrial queueing system, in which customer are now aware when the server becomes available and have to actively check it.
Strategic customers decide when to check considering queue length and the age of their information. We use Dynamic Programming approach to construct customers' cost functions and obtain optimal and/or Nash Equilibrium strategies.
Joint work with Ricky Roet-Green (U. Rochester)
Yutaka Sakuma (National Defense Academy of Japan) - An arrival distribution for the equilibrium expected waiting time in a discrete-time single-server queue with acceptance period and Poisson population of customers
November 07, 2018
This study considers a discrete-time first-come first-served single-server queue with acceptance period. Customers arrive at the system within the acceptance period. The total number of arriving customers is Poisson distributed, and their service times are independent and identically distributed with a general distribution. It is assumed that each customer chooses its arrival time slot with the goal of minimizing its expected waiting time. For this queueing model, we obtain an arrival distribution of customers for the equilibrium expected waiting time, called an equilibrium arrival distribution for short. Through some numerical examples, we show that the large variation of service times causes the rush of customers to the opening slot. Furthermore, we propose a simulation model which will exhibit an arrival time distribution similar to the one in equilibrium.
Mariska Heemskerk (UvA)
October 25, 2018
Queueing networks often face highly variable (i.e. overdispersed) arrival streams, to the point where the standard assumption of Poissonian arrivals is not statistically valid anymore.
Taking an overdispersed arrival process as a leading example with the objective to approximate its tail distribution, we study the probability $\xi_n(u):={\mathbb P}\left(C_n\geqslant u n \right)$ for a composition of L\'{e}vy processes $C_n$. Here $C_n:=A(\psi_n B(\varphi_n))$ consists of L\'{e}vy processes $A(\cdot)$ and $B(\cdot)$, and scaling variables $\varphi_n$ and $\psi_n$. The latter are non-negative sequences such that $\varphi_n \psi_n =n$ and $\varphi_n\to\infty$ as $n\to\infty$. Two timescale regimes can arise: a `fast' regime in case $\varphi_n$ is superlinear (hence $\psi_n \to 0$), and a `slow' regime, in the setting where $\varphi_n$ is sublinear (in which case $\psi_n$ must be sublinear too).
We provide the exact asymptotics of $\xi_n(u)$ as $n\to\infty$ for both regimes, relying on change-of-measure techniques in combination with Edgeworth-type estimates. The asymptotics have an unconventional form: the exponent contains the commonly observed linear term, but may also contain sublinear terms. When using the asymptotic expression as an approximation for the pre-limit probability, the retrieved refinements should thus improve the accuracy of the approximation. We show that under mediocre timescale seperation this is indeed the case.
Madelon de Kemp (UvA) - The convex order and appointment sequencing
October 10, 2018
This talk will consist of two parts. The first part is a short tutorial about the convex order on random variables. Intuitively, this order compares the spread of random variables with the same mean, but in a more detailed way than by just looking at the variance.
The second part is about our research in appointment scheduling, and how the convex order plays a role in our results. In appointment scheduling problems, the deterministic arrival times of patients in a single-server queue should be determined. This should be done such that there is both little idle time and little waiting time. Part of this problem is the sequencing problem, in which the order in which different patients arrive should be determined.
The so-called smallest-variance-first rule, which sequences patients in order of increasing variance of their service durations, is often found to perform better than other heuristics. Under some simplifying assumptions, we will consider the performance of the smallest-variance-first rule. By comparing an upper bound on the expected waiting times under this rule with a lower bound valid for any sequence, we will able to bound the relative difference in performance between the smallest-variance-first rule and the optimal sequence.
Phil Whiting (Macquarie University) - Probability and Breaking the Enigma Codes
October 10, 2018
When: 12:00
Where: L120 CWI
Part 1:
This talk gives a brief description of the 3 rotor wheel version of the Enigma machine and a probability model for the encoder. It is then explained how breaks could be obtained due to a particular quirk that occurred because of a certain German signalling protocol. These breaks were made well before the start of the Turing-Welchman bombe which began in late summer 1940.
Nikki Sonenberg (Antwerp University) - Networks of interacting stochastic fluid models
September 26, 2018
Stochastic fluid models have been widely used to model the level of a resource that changes over time, where the rate of variation depends on the state of some continuous time Markov process. Latouche and Taylor introduced an approach, using matrix analytic methods and the reduced load approach for loss networks, to analyse networks of fluid models all driven by the same modulating process where the buffers are infinite. We extend the method to networks involving finite buffer models and illustrate the approach by deriving performance measures for a simple network as characteristics such as buffer size are varied. Our results provide insight into the situations where the infinite buffer model is a reasonable approximation to the finite buffer model.
Christa Cuchiero (University of Vienna)-Infinite dimensional polynomial processes
June 24, 2018
Motivated from high and infinite dimensional problems in mathematical finance, we consider infinite dimensional polynomial processes taking values in certain space of measures or functions. We have two concrete applications in mind: first, modeling high or even potentially infinite dimensional financial markets in a tractable and robust way, and second analyzing stochastic Volterra processes, which recently gained popularity through rough volatility models and ambit processes. The first question leads to probability measure valued polynomial diffusions and the second one to Markovian lifts of polynomial Volterra processes. For both cases we provide existence results and a moment formula.
Conrado da Costa (Leiden University) - Random Walks in Cooling Random Environments
June 06, 2018
Random Walks in Dynamical random environment are random walks whose transition rules depend on the time and the position of the walker. In this talk we consider a specific kind of Dynamic random environment, the Cooling random environment, as introduced in the paper "Random walks in cooling random environments" by Avena and den Hollander.
In this talk we discuss two main new results: the Strong Law of Large Numbers and a quenched Large deviation principle for the Random Walk in the Cooling random Environment. For the proof of these two results, we present two auxiliary results. The first, an ergodic theorem for cooling random variables and the second, a concentration result for the cumulant generating function of the static Random Walk in the random environment.
References:
https://arxiv.org/abs/1610.00641
https://arxiv.org/abs/1803.03295
Santi Duran (Toulouse) - Asymptotic Optimal Control of Markov-Modulated Restless Bandits
June 03, 2018
In this talk we will discuss optimal control subject to changing conditions (a changing environment). This is an area that recently received a lot of attention as it arises in numerous situations in practice. Some applications being cloud computing systems with fluctuating arrival rates, or the time-varying capacity as encountered in power-aware systems or wireless downlink channels. To study this, we focus on a restless bandit model, which has proved to be a powerful stochastic optimization framework to model scheduling of activities. This work is a first step to its optimal control when restless bandits are subject to changing conditions.
We consider the restless bandit problem in an asymptotic regime, which is obtained by letting the population of bandits grow large, and letting the environment change relatively fast. We present sufficient conditions for a policy to be asymptotically optimal and show that a set of priority policies satisfies these. Under an indexability assumption, an averaged version of Whittle's index policy is proved to be inside this set of asymptotic optimal policies. The performance of the averaged Whittle's index policy is numerically evaluated for a multi-class scheduling problem.
This talk is based on a joint work with Maaike Verloop, for details check https://dl.acm.org/citation.cfm?id=3179410 or https://hal.laas.fr/hal-01696329/document.
Bart Kamphorst (CWI) - Heavy-traffic analysis of the Foreground-Background scheduling policy
May 23, 2018
We consider the steady-state distribution of the sojourn time of a job entering an M/G/1 queue with the Foreground-Background scheduling policy in heavy traffic. The growth rate of its mean, as well as the limiting distribution, are derived under broad conditions. Assumptions commonly used in extreme value theory play a key role in both the analysis and the results. In the presentation, we emphasise the intuition behind the results and discuss how the obtained insights might be used in the analysis of other scheduling policies.
Time: 11:00 - 12:00
Location: F3.20 of KdVI (Science Park 105-107, 3rd floor - entrance via Nikhef).
Arnoud den Boer (UvA) - Behavioral aspects in dynamic pricing and learning
May 16, 2018
In this talk, I’d like to discuss some recent findings on optimal pricing in view of various behavioral aspects of consumers that make the price optimization complex and interesting: strategic waiting of consumers, and the influence of reference effects. In addition I’d like to show how reference effects can be accounted for in data-driven pricing algorithms.
Time: 11:00 - 12:00
Location: F3.20 of KdVI (Science Park 105-107, 3rd floor - entrance via Nikhef).
Eyal Castiel (Institut Supérieur de l'Aéronautique et de l'Espace (ISAE)) - Queuing Networks and separation of time scales using Log-Sobolev inequality
May 02, 2018
When considering a Markov process with two distinct component, it can happen that they evolve on different time scales (one is fast and the other is slow). In some cases, we can hope that the fast one "averages" so that it only influences the slow one through its steady state mean. When that is the case we say there is a separation of time scales (or homogenization).
During this talk, I will present a work in progress, developing a novel method to obtain condition on the joint dynamic to a time scale separation using functional inequalities (Log-Sobolev and Gronwall). As an application example we'll expose different scheduling algorithm for wireless networks with a focus on CSMA-Queue based algorithms. We will also see how to derive stability using homogenization in this case.
David Koops - Nonparametric estimation for infinite-server queues with nonhomogeneous Poisson arrivals
April 18, 2018
In this talk I will consider a particular partial information problem, which is in the interface of queueing theory and nonparametric statistics. More precisely, I will consider an infinite server queue with a nonhomogeneous Poisson arrival process, of which the queue length process can be observed. The problem is to estimate the distribution function and expected value of the service time G. A complicating factor is that jobs are not identifiable: arrival epochs cannot be matched to their corresponding departure epochs. I will show how estimators can be constructed, and provide upper bounds on the bias and variance under the assumption that G is in a certain class of smooth functions. Some examples and simulations will be discussed.
Liron Ravner - Estimating the input of a queue by Poisson sampling of the workload process
April 04, 2018
Inferring the statistical properties of queueing systems by observing the workload is a challenging task due to the elaborate dependence between transient samples. In particular, likelihood functions are typically intractable. We consider the problem of estimating the exponent function of the Laplace-Stieltjes Transform (LST) of the input process to a Lévy driven queue. The workload of the queue is observed at random times according to an independent Poisson process. We suggest a non-parametric estimation method that relies on the empirical Laplace transform of the workload. This is achieved by using a generalized method of moments approach on the conditional LST of the workload sampled after an exponential time. The consistency of the method requires an intermediate step of estimating a constant that is related to both the input distribution and the sampling rate. To this end, for the case of an M/G/1 queue, we construct a partial maximum likelihood estimator and show that it is consistent and asymptotically normal. For spectrally positive Lévy input we construct a biased estimator for the intermediate step by considering only high workload observations above some threshold. A bound on the bias is provided and we discuss the tradeoff between the bias and variance of the estimator with respect to the chosen threshold. We further discuss how this framework can be useful in applications such as stability detection and dynamic pricing.
Joint work with Onno Boxma and Michel Mandjes
Jacobien Carstens - Symmetry in Markov chains for sampling graphs with fixed degree sequence
March 28, 2018
The sampling of graphs with fixed degree sequence has become an important quantitative tool in network analysis. For instance, it is used in community detection and motif finding; techniques which derive meaning from a network’s topology. Mathematically, the sampling of bipartite graphs with fixed degree sequence is equivalent to sampling binary matrices with fixed row and column sums. Sampling matrices is seen as one of the most useful null-model approaches in ecology in deciding if an observed data matrix shows extremal behaviour.
Even though sampling algorithms are widely used by practitioners, the underlying theory has not yet been fully developed. In particular, there is no known method which can be proven to sample both uniformly and efficiently (i.e. runs in polynomial time), yet existing algorithms are used to create samples for statistical analysis of real-world data. There is no guarantee that those samples are unbiased.
In this talk we focus on Markov chain approaches to this problem, where close-to-random graphs are generated by making a large number of small changes to a given graph. In particular, we discuss two results from recent work on analysing the mixing time of such Markov chains. The first result is a state space decomposition that allows for a mixing time comparison of the well-known switch chain and of the intuitively faster Curveball algorithm. The second result reduces the size of the state space by removing certain redundant symmetries. This improves the mixing time and makes certain previously intractable problems finite.
Céline Comte (Nokia Bell Labs France and Télécom ParisTech) - Performance of Balanced Fairness in Resource Pools: A Recursive Approach
March 21, 2018
Understanding the performance of a pool of servers is crucial for proper dimensioning. One of the main challenges is to take into account the complex interactions between servers that are pooled to process jobs. In particular, a job can generally not be processed by any server of the cluster due to various constraints like data locality. In this paper, we represent these constraints by some assignment graph between jobs and servers. We present a recursive approach to computing performance metrics like mean response times when the server capacities are shared according to balanced fairness. While the computational cost of these formulas can be exponential in the number of servers in the worst case, we illustrate their practical interest by introducing broad classes of pool structures that can be exactly analyzed in polynomial time. This extends considerably the class of models for which explicit performance metrics are accessible.This is a joint work with Thomas Bonald (Télécom ParisTech) and Fabien Mathieu (Nokia Bell Labs France).
Arnaud Le Ny (Université Paris Est) - Gibbs States for 2d-long-range Ising models
March 14, 2018
In this talk, we shall review old and new results about Gibbs measures in dimension 2 for Ising models, in the classical nearest neighbours case but also for some long-range polynomially decaying interactions. We shall focus on the existence of so-called Dobrushin States, that are non-translation invariant extremal states known to exist in 3d and related to the fluctuations of an interface got by prescribing mixed boundary conditions.This is joint work in progress with L. Coquille (Grenoble), A. van Enter (Groningen) and W. Ruszel (Delft).
Nicos Starreveld - Introduction to Stein's method
March 07, 2018
Stein’s method was initially conceived by Charles Stein to provide errors in the approximation by the normal distribution of the distribution of the sum of dependent random variables of a certain structure. In this talk I will present some basic techniques and results related to Stein's method. I will present in detail the case X_1,X_2,... are i.i.d random variables and the case they have some dependency structure. My presentation is based on Chapters 1-3 from "Fundamental of Stein's method" by Nathan Ross and "Stein's method for concentration inequalities" by Sourav Chatterjee.
Sonja Cox - Decoupling inequalities and stochastic integration
February 28, 2018
In order to define a stochastic integral, one needs to get control over its moments. If the state-space is infinite-dimensional and one is interested in norms other than a Hilbert space norm, then decoupling techniques are needed to obtain this control. If the last two sentences sound a bit cryptic, please come to my talk and I will explain!
Marijn Jansen - A gentle introduction to the Skorokhod topology and weak convergence of stochastic processes
February 21, 2018
About a year ago Nicos Starreveld gave a talk on weak convergence. I would like to complement his talk by taking a closer look at weak convergence of stochastic processes. More specifically, I will discuss why the Skorokhod topology is the natural setting for weak convergence of stochastic processes, and try to convince you that it is actually quite easy to understand and to work with. If time permits, I will give an example of a G/M/infty queue converging weakly to a stochastic differential equation in the Skorokhod topology.
Philipp Harms - A Markovian perspective on fractional Brownian motion
February 15, 2018
Many fractional processes, including fractional Brownian motion, can be represented as linear functionals of an infinite-dimensional Markov process. Intuitively, the state of the Markov process captures the entire history of the fractional process. This representation leads to efficient simulation schemes of fractional processes. Moreover, as an application in mathematical finance, it allows one to construct tractable financial models with interesting fractional features.
Daphne van Leeuwen - Optimal (batch) dispatching in a tandem queue
February 07, 2018
We investigate a Markovian tandem queueing model in which service to the first queue is provided in batches. The main goal is to choose the batch sizes so as to minimize a linear cost function of the mean queue lengths. This model can be formulated as a Markov Decision Process (MDP) for which the optimal strategy has nice structural properties.
In principle we can numerically compute the optimal decision in each state, but doing so can be computationally very demanding. A previously obtained approximation is computationally efficient for low and moderate loads, but for high loads also suffers from long computation times.
In this talk I will show how we exploit the structure of the optimal strategy and develop heuristic policies motivated by the analysis of a related controlled fluid problem. The fluid approach provides excellent approximations, and thus understanding, of the optimal MDP policy. The computational effort to determine the heuristic policies is much lower and, more importantly, hardly affected by the system load. The heuristic approximations can be extended to models with general service distributions, for which we numerically illustrate the accuracy.
Jaap Storm - Congestion phenomena and a traffic model for a roundabout.
January 31, 2018
To optimally design and operate road networks, mathematical models play a crucial role. They help shedding light on congestion phenomena, and on the efficacy of policies to remedy them. Because of this, in recent years there has been a lot of research in the area of traffic flow theory, including the performance analysis of road structures. There has however not been a lot of research on so-called roundabouts; a specific form of intersection design where vehicles navigate in one direction, usually in a circular way, around a central island and that gives priority to vehicles on the roundabout.
In this talk I will present a new traffic model for a roundabout which is a hybrid between a cellular automaton and a queueing network. During the talk I will discuss our analysis of the model and complications. In particular there is some focus on how to prove stability of the model, where we apply a coupling and fluid techniques.
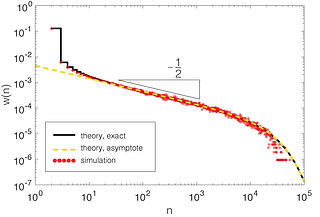
Ivan Kryven - Identifying the size distribution of connected components in sparse random graphs with arbitrary degree distributions
January 24, 2018
This talk discusses the problem of identifying the size distribution of connected components in sparse random graphs with arbitrary degree distributions.
Such a problem naturally arises in various applied disciplines, as for instance: material science, chemistry, social physics and economics, where one often has access only to local information of an empirical network, whereas the global properties of this network are to be reconstructed.
The talk is organised into three parts: Firstly, by applying Joyal's theory of species, the problem will be stripped of its graph-theoretical context and reformulated in terms of stochastic sums involving i.i.d. random variables. Secondly, an exact equation for the size distribution will be proposed together with a relevant asymptotic analysis for large components. Thirdly, the whole framework will be generalised to cover directed graphs and graphs with multiple types of symmetric edges (also known as multiplexes).
The talk will be finalised with a few application examples of this theory.
Sindo Nunez Queija - Boundary value problems and applications in queueing theory
January 10, 2018
Functional analysis plays a central role in the analysis of queueing systems. For a a large class of two-dimensional Markov processes, the stationary distribution can be characterized as the solution to a so-called boundary value problem. In this talk we will explore the basics of the theory of boundary value problems and illustrate their use in queueing theory. The approach relies on the use of transforms (typically probability generating functions and Laplace-Stieltjes transforms) to translate balance equations into a functional equation in terms of the unknown transform. Knowing that the transform belongs to a (multi-dimensional) probability distribution ensures that it is analytic in a some specified domain of the complex plane (i.e., PGFs are analytic inside the unit disc and LSTs are analytic in the half plane of complex numbers with positive real part). In many examples this is enough to uniquely characterize the transform as a complex integral.We will illustrate in detail the analysis of one particular queueing problem that can be reduced to the solution of a Riemann-Hilbert boundary value problem.
Leonardo Rojas-Nandayapa - Fitting phase-type scale mixtures to heavy-tailed risks
December 13, 2017
We consider the fitting of heavy tailed risk distributions with a special attention to distributions with a non-standard shape in the "body" of the distribution. To this end we consider a dense class of heavy tailed distributions introduced recently, employing an EM algorithm for the maximum likelihood estimates of its parameters. We present methods for fitting to observed data, histograms, censored data, as well as to theoretical distributions. Numerical examples are provided with simulated data and a benchmark reinsurance dataset. We empirically demonstrate that our model can provide excellent fits to heavy-tailed data/distributions with minimal assumptions.
Stephen Davis - Noisy Graph Matching and Graph Dissimilarity Measures
December 06, 2017
Inexact graph matching is a flexible technique to compare `noisy' graphs, and gives rise to dissimilarity measures that can define a formal distance. We take advantage of this in the field of biometrics, with diverse applications ranging from the infant biometric problem (finding a physical trait that can reliably identify children aged 0-2 years) to improving the training of fingerprint experts in law enforcement.
Andrea Roccaverde - Breaking of ensemble equivalence in complex networks
November 29, 2017
In this talk I will speak about the phenomenon of breaking of ensemble equivalence in complex networks. For many system in statistical physics the microcanonical and canonical ensemble are equivalent in the thermodynamic limit, but not for all. The goal is to classify for which classes of complex networks with topological constraints, breaking of ensemble equivalence occurs. We consider the simple case in which we fix the number of links and then we move to the configuration model (we fix the degree of each vertex). Then we study a more general setting with an arbitrary number of intra-connected and inter-connected layers, thus allowing modular graphs with a multi-partite, multiplex, time-varying, block-model or community structure. We give a full classication of ensemble equivalence in the sparse regime, proving that breakdown occurs as soon as the number of constrained degrees is extensive in the number of nodes, irrespective of the layer structure. In addition, we derive an explicit formula for the specic relative entropy and provide an interpretation of this formula in terms of Poissonisation of the degrees.
Asma Khedher - An introduction to backward stochastic differential equations
November 22, 2017
Backward stochastic differential equations (BSDEs) appear in numerous problems in finance as for example hedging and control theory problems. We aim at introducing the basic theory of BSDEs and study the relation to partial differential equations.
Jevgenijs Ivanovs - Zooming in on a Levy process at its supremum
November 16, 2017
Let M and $\tau$ be the supremum and its time of a Levy process X on some finite time interval. It is shown that zooming in on X at its supremum, that is, considering $((X_{\tau+t\varepsilon}-M)/a_\varepsilon)_{t\in\mathbb R}$ as $\varepsilon$ tends to 0, results in $(\xi_t)_{t\in\mathbb R}$ constructed from two independent processes corresponding to some self-similar Levy process $\widehat X$ "conditioned" to stay positive and negative. This holds when X is in the domain of attraction of $\widehat X$ under the zooming-in procedure as opposed to the classical zooming-out of Lamperti (1962) As an application of this result we provide a limit theorem for the discretization errors in simulation of supremum and its time, which extends the result of Asmussen et al. (1995) for the Brownian motion.Additionally, I will briefly discuss Levy processes reflected to stay in a strip and the associated discretization errors, which is based on joint work with Soren Asmussen.
Peter Spreij - An Introduction to Risk Measures
November 15, 2017
The most popular risk measure is value at risk (VaR), a quantile. VaR satisfies a number of properties of a so called monetary risk measure, but it is in general not convex, i.e. (contrary to common sense) diversification of an investment portfolio may be discouraged. We will see other risk measures (e.g. average value at risk) that are convex, or even coherent, i.e. they satisfy a number of axioms, by definition. Other topics to be treated are acceptance sets and their duality relation with risk measures, robust representations of risk measures, in terms of nonlinear expectations or expectations w.r.t. finitely additive measures. Continuity (w.r.t. weak* topology) properties of risk measures are also treated, and their relation to representation properties. Perhaps, also relations with statistical testing theory (Neyman-Pearson) will be explained. The presentation only requires basic knowledge of probability.
Guido Lagos - On the Euler discretization error of Brownian motion about random times
November 08, 2017
In this talk we study the simulation of barrier-hitting events and extreme events of Brownian motion, when using a discretization on an equidistant time mesh. Specifically, we study the times and position of the discretized Brownian motion in these events and compare it to the ones for the "real" Brownian motion. We establish new results on weak convergence of the (normalized) errors of time and position in all these cases, and give explicit analytic expressions for the limiting distributions. In doing this we derive new results on diffusion approximations of Gaussian random walks by Brownian motions. More importantly, our results give new insight on the connection between several works in the literature dating back to the 60's where the constant $-\zeta(1/2)/\sqrt{2\pi}$ has appeared, where $\zeta$ is the Riemann zeta function.
Uri Yechiali - Tandem Jackson Networks, Asymmetric Inclusion Processes and Catalan Numbers
October 11, 2017
The Tandem Jackson Network is a system of n sites (queues) in series, where single particles (customers, jobs, packets, etc.) move, one by one and uni-directionally, from one site to the next until they leave the system (think, for example, on a production line, or on a line in a cafeteria). When each site is an M/M/1 queue, the Tandem Jackson Network is famous for its product-form solution of the multi-dimensional distribution function of the sites' queue-sizes.
In contrast, the Asymmetric Inclusion Process (ASIP) (introduced recently by Reuveni, Eliazar and Yechiali) is a series of n Markovian queues (sites), each with unbounded capacity, but with unlimited-size batch service. That is, when service is completed at site k, all particles present there move simultaneously to site k+1, and form a cluster with the particles present in the latter site (think, for example, on cars travelling on a single-lane road, forming sets of convoys, where a faster convoy joins the tail of its preceding slower one, and the two convoys continue moving as a single larger convoy).
We analyze the ASIP and show that its multi-dimensional Probability Generating Function (PGF) does not posses a product-form solution. We then present a method to calculate this PGF. We further show that homogeneous systems are ‘optimal’ and derive limit laws (when the number of sites becomes large) for various variables (e.g. busy period, draining time, etc.).
Considering the occupancies of the sites (‘queue sizes’) we show that occupation probabilities in the ASIP obey a discrete two-dimensional boundary-value problem. Solving this problem we find explicit expressions for the probability that site k is occupied by m particles (m=0,1,2,…).
Catalan's numbers are shown to naturally arise in the context of these occupation probabilities.
Jan van Waaij - The performance of nonparametric Bayesian methods for diffusions
September 11, 2017
In Bayesian statistics the inference is done via the posterior, that is the probability distribution of the parameter space given the data. The parameter space is equipped with a probability distribution called the prior and the posterior is calculated with the help of the Bayes formula. For parametric (i.e. finite dimensional) models the Bernstein-von Mises theorem guarantees under regularity assumptions that the posterior convergences to a normal distribution concentrated around the true parameter. For nonparametric models (i.e. the parameter belongs to some infinite dimensional function space) this is in general not true anymore. The posterior may wander around putting mass aimlessly all over the place, even for seemingly reasonable models and priors. An important point of research therefore is the asymptotic behaviour of the posterior. We study the asymptotic behaviour of a diffusion model. We consider continuous time observations \{X_t:t\in[0,T]} of a stochastic differential equation (SDE) dX_t=\theta(X_t)dt+dW_t,
where \theta:R—>R is measurable, one-periodic and \int_0^1\theta(x)^2dx<\infty. The space of this functions being denoted by L^2(T). In this talk I'll discuss several choices of priors on L^2(T). We’ll see that this performance depends on the (Sobolev-)smoothness of the true function. We'll discuss several methods to obtain adaptivity to the unknown smoothness of the true parameter.
This talk is based on joint work with Frank van der Meulen (Delft University of Technology), Moritz Schauer (Leiden University) and Harry van Zanten (University of Amsterdam) and the publication van Waaij & van Zanten (2016, https://projecteuclid.org/euclid.ejs/1457382316) and recent unpublished work.
Mariska Heemskerk - Queueing systems in a random environment: asymptotic analysis and MOL staffing
July 03, 2017
In this talk we consider queueing systems in a random environment. As the latter entails that no communication between customers and servers occurs, the uncertain arrival stream is usually modeled under the assumption of Poisson arrivals in this setting. Note that in some cases the often used (nonhomogenous) Poisson process fails to capture the dynamics of an arrival process: not only do some systems face arrival streams that are almost deterministic (mean $>>$ variance), there are others, which are of special interest to us, that have to deal with highly variable arrivals (mean $<<$ variance) -- they face overdispersion. The model we propose here is a comprehensive yet simple model for overdispersed arrival processes which can additionally handle nonhomogeneity and dependency between arrival rates of subsequent time slots. The random environment is modeled by a mixed Poisson process, where the random parameter takes a new value every time slot of fixed size.
We are interested in the effect of such an arrival process on the performance of an infinite-server system. As it turns out, in a rapidly changing random environment (i.e., slot size is small relative to system size) the overdispersion of the arrival process hardly affects system behavior, whereas in a slowly changing random environment it is fundamentally different. This general finding applies to both the central limit and the large deviations regime. Having studied these effects, we apply our results via MOL staffing for the corresponding finite-server counterpart. The resulting staffing procedure stabilizes system performance rather well.
David Koops - Externally and endogenously excited arrival processes in queueing theory
June 26, 2017
An often employed assumption in queueing theory is that arrivals occur according to a Poisson process with a fixed rate. There is much evidence, however, that this assumption is often false. Instead, in this talk I will consider two alternative arrival processes: (1) a Poisson process of which the rate itself is a stochastic shot-noise process, (2) a self-excited (Hawkes) process. These processes will serve as input to an infinite server queueing system.
In the first model there are sudden shocks (increases) in the rate at Poisson epochs, after which the rate tends to revert back to "normal" values. The interpretation is that there are external events which lead to a temporary increase of demand. In the second model the increases in the rate are not only due to external events, but also due to arrivals to the queue itself. This effect is sometimes observed in practice: for example, a somewhat full restaurant is more likely to attract customers than an empty one. Also, in the financial markets this type of "herding behaviour" is often observed, for example in buying and selling of stocks or bitcoins.
Madelon de Kemp - Performance of the smallest-variance- first rule in appointment sequencing
June 26, 2017
In appointment scheduling problems, the deterministic arrival times of patients in a single-server queue should be determined. This should be done such that there is both little idle time and little waiting time. Part of this problem is the sequencing problem, in which the order in which different patients arrive should be determined.
The so-called smallest-variance-first rule, which sequences patients in order of increasing variance of their service durations, is often found to perform better than other heuristics. Under some simplifying assumptions, we will consider the performance of the smallest-variance-first rule. By comparing an upper bound on the expected waiting times under this rule with a lower bound valid for any sequence, we will be able to bound the difference in performance between the smallest-variance- first rule and the optimal sequence.
César A. Uribe - Learning for Cooperative Inference
June 25, 2017
We study the problem of cooperative inference where a group of agents, interacting over a network, seeks to estimate a joint parameter that explains a set of observations over the network. Agents are agnostic to the network topology and the observations of other agents. The complex interactions on the network result in intractable computations for centralized estimation approaches. We explore a variational interpretation of the Bayesian posterior, and its relation with the stochastic mirror descent algorithm, to propose a set of new distributed learning algorithms. The beliefs generated by the proposed algorithms concentrate around the true parameter exponentially fast. We provide explicit non-asymptotic bounds for this concentration. Particularly, we develop explicit and computationally efficient algorithms for observation models belonging to the exponential family.
Brendan Patch - Detecting Markov Chain Instability: A Monte Carlo Approach
June 12, 2017
We devise a Monte Carlo based method for detecting whether a non-negative Markov chain is stable for a given set of potential parameterizations. More precisely, for a given set in parameter space, we develop an algorithm that is capable of deciding whether the set has a subset of positive Lebesgue measure for which the Markov chain is unstable. The approach is based on a variant of simulated annealing, and consequently only mild assumptions are needed to obtain performance guarantees. I will illustrate the usage of our algorithm on models of communication networks.
This is joint work with Michel Mandjes (University of Amsterdam) and Neil Walton (The University of Manchester).
Janusz Meylahn - Synchronization and the Kuramoto model
May 22, 2017
I will motivate the interest in studying synchronization using the Kuramoto model and give an introduction to the model as it was first introduced by Kuramoto. Following this I will summarize results on the limiting equation for the density of oscillator phases as the number of oscillators grows to infinity as well as results on the stationary solution to this equation. Since the stationary solution might not be unique, I will discuss the conditions which determine the types of solutions that are possible and their stability. If time permits I will present the Kuramoto model on a network with community structure and highlight the research challenges that arise in this setting.
Abhishek - Waiting time and heavy-traffic analysis of M^X/G/1 type queuing models with dependent service durations
May 08, 2017
We consider a single-server queue with N types of services, in which, customers arrive according to a batch Poisson process. The service times of customers have general distribution functions and are correlated. The correlations are due to the different service types, which form a Markov chain that itself depends on the sequence of service lengths. Our work is motivated by an application of the model to road traffic, where a stream of vehicles on a minor road merges with a stream on a main road at an unsignalized intersection such that the merging times of two subsequent vehicles on the minor road are dependent.
Based on the results from a previous paper on the steady-state distribution of the queue length, we derive the waiting time and sojourn time distributions. The waiting times and sojourn times of customers depend on their positions in the batches, as well as on the type of service of the first customers in their batches. We also determine the heavy-traffic distribution of the scaled stationary queue length.
Hakan Guldas - Random walks on dynamic configuration model
May 01, 2017
In this talk, first I will introduce dynamic configuration model which is a dynamic random graph model in discrete time. Then, I will go into details of our results about mixing times of simple random walks on dynamic configuration model. The key property of the dynamic configuration model is that the degrees of the vertices do not change over time. Thanks to this property, the notion of stationary distribution for the random walk makes sense and mixing occurs although the random walk is not Markovian. The results I will give identify the behaviour of mixing times in terms of the proportion of edges that changes at every step of graph dynamics when the number of vertices is large. These results are part of a joint work with Luca Avena, Remco van der Hofstad and Frank den Hollander.
Fiona Sloothaak - Cascading failures and random walks: a powerful connection
April 10, 2017
Cascading failure models are used to describe systems of interconnected components where failures possibly trigger subsequent failures of other components. Despite the deceptively simple appearance of these models, they capture an extraordinary richness of different behaviors and have proven to be effective in a wide range of applications. Our inspiration is drawn from power outages in electric transmission systems. As these networks continue to increase in complexity and volatility, a fundamental understanding of the risks of cascading failures becomes of critical importance to guarantee and maintain a high reliability.
Motivated by the above issues, we examine the probability that the number of failed components exceeds a threshold in an asymptotic regime, i.e. where the network size grows large. We are particularly interested in identifying conditions under which this tail exhibits power-law behavior, as is commonly encountered in empirical data analysis of blackout sizes. Our approach exploits an equivalent random-walk representation, where the objective translates to deriving the asymptotic probability that the first-passage time over a moving boundary exceeds the threshold, conditioned that the random walk returns to zero at a (specific) later point in time. Depending on the boundary, this yields a possible phase transition in the behavior when the threshold is close to the network size.
Joint work with Bert Zwart, Vitali Wachtel and Sem Borst.
Jacobien Carstens - The Curveball algorithm: A fast and flexible approach to sampling networks with fixed degree sequence.
April 03, 2017
Randomisation of binary matrices has become an important quantitative tool in modern computational biology. The equivalent problem of generating random directed networks with fixed degree sequences is used in several network analysis techniques such as community detection and motif finding. It is however challenging to generate truly unbiased random graphs with fixed degree sequence.
In this talk we focus on Markov chain approaches to network randomisation. We discuss the well-known switching model and the more recently introduced Curveball algorithm. We show that both frameworks can be used to randomise a variety of network classes and prove that both algorithms converge to the uniform distribution.
However, the main question for both theoreticians and practitioners remains unanswered: that is, in all but some special cases it is unknown how many steps the Markov chains needs to take, in order to sample from a distribution that is close to uniform. Experimental results suggest that the Curveball algorithm converges faster. If time permits we will discuss current work towards proving that the Curveball algorithm outperforms the switching model.
Sonja Cox - Weak convergence for semi-linear SPDEs
March 13, 2017
In numerical analysis for stochastic differential equations, a general rule of thumb is that the optimal weak convergence rate of a numerical scheme is twice as large as the optimal strong convergence rate. However, for SPDEs the optimal weak convergence rate is difficult to establish theoretically. Recently, progress was been made by Jentzen, Kurniawan and Welti for semi-linear SPDEs using the so-called mild It\^o formula. We consider this approach for wave equations, and (if time remains) discuss the necessity of extending the theory to the Banach space setting in order to obtain optimal rates when the non-linear terms are given by Nemytskii operators.
Nicos Starreveld - Weak convergence of probability measures
March 06, 2017
In this Tutorial I will present some basic results on weak convergence of probability measures. I will rely on the, classical by now, book of Patrick Billingsley "Convergence of probability measure". I will treat Chapters 1 and 2. I will state some basic definitions and prove Prohorov's theorem. I will present the main theorem concerning weak convergence on the space of continuous function on [0,1] and discuss some major results derived from it, amongst other the existence of a Wiener measure and Donsker's theorem. If time allows I will present some recent research results (by people from the UvA and CWI) derived using these techniques.
Chang-Han Rhee - Sample-Path Large Deviations for Heavy-Tails: the Principle of Multiple Big Jumps
February 27, 2017
Many rare events in man-made networks exhibit heavy-tailed phenomena: for example, file sizes and delays in communication networks, financial losses, and magnitudes of systemic events such as the size of a blackout in a power grid. While the theory of large deviations has been wildly successful in providing systematic tools for understanding rare events in light-tailed settings, the theory developed in the heavy-tailed setting has been mostly restricted to model-specific results or results pertaining to events that are caused by a single big jump. In this talk, we present our recent result that goes beyond such restrictions and establish sample-path large deviations for a very general class of rare events associated with heavy-tailed random walks and Levy processes.
Joint work with Jose Blanchet (Stanford University) and Bert Zwart (CWI).
Krzysztof Bisewski - Controlling the time-discretization error for the supremum of Brownian Motion.
February 20, 2017
It is often of interest to find the tail distribution of the supremum of a real stochastic process. When an explicit expression for the distribution is unavailable it is usually approximated numerically, using various rare event simulation techniques. For most of the available methods the underlying process needs to be discretized in time. However, it requires a surprisingly dense discretization to achieve a negligible error. This in turn results in a computationally expensive simulation. For the standard Brownian Motion we illustrate how a naive discretization choice influences the discretization error and propose a solution to circumvent that problem using an adaptive placement of grid-points.
Thomas Taimre - Exploiting asymptotic structure for efficient rare-event estimation for sums of random variables
February 13, 2017
We consider the problem of estimating the right-tail probability of a sum of random variables when the density of the sum is not known explicitly, but whose asymptotic behaviour is known. We embed this asymptotic structure into a simple importance sampling estimator, in which we consider the radial and angular components of the distribution separately. By design, this estimator has a bounded relative error when the marginal tails decay exponentially. Moreover, we present a procedure to obtain a `good' approximation to the angular component as a mixture of Dirichlet distributions by using Bernstein polynomial approximation (cf. the Weierstrass approximation theorem). The estimator and procedure are applicable in both the heavy- and light-tailed settings, as well as for dependent and independent summands. We illustrate the approach with a series of examples. This is joint work with Patrick Laub.
Bohan Chen - Importance sampling of heavy-tailed iterated random functions
February 06, 2017
We consider the problem of constructing efficient rare-event simulation algorithm for estimating the tail of a stochastic perpetuity. Stochastic perpetuity can be found in the analysis of probabilistic algorithms and financial mathematics. It also arises naturally when we consider the steady-state distribution of a Markov chain constructed by iterated random affine functions. In this work, we provide a consistent simulation estimator using state-dependent importance sampling for the case, where the increments of the underlying random walk are heavy-tailed, and hence, the so-called Cramér condition is not satisfied. We show that under natural conditions, our estimator is strongly efficient. Furthermore, we extend our method to a more general case, where the underlying Markov chain is constructed by iterated random Lipschitz functions.
Julia Kuhn - On deriving exact asymptotics for applications in queuing
January 09, 2017
Large deviations (LD) theory can provide useful asymptotically accurate approximations for the probability that a sum of random variables assumes a rare value. Rare-event probabilities encountered in practice, however, often do not allow for a direct application of known LD results. In this talk I will show how in a number of simple steps one can sometimes leverage the celebrated Bahadur-Rao theorem to derive asymptotically equivalent (exact) expressions for such rare-event probabilities. In particular I will present an example from K., Mandjes, and Taimre that is related to the comparison of order statistics of sample-means stemming from two different distributions. More briefly, I will discuss that with the same method we can derive the asymptotic tail distribution of a doubly stochastic Poisson arrival process (Heemskerk, K., Mandjes). In addition, if time permits, I will show that the importance sampling procedures suggested by these LD results are asymptotically optimal.
Peter Kovacs - Adapting distributed data flow protocols to vehicle-actuated traffic control policies
December 05, 2016
The advancement in technology over the recent decade allowed the collection and processing of data from traffic conditions on roads in real time. With the enormous amount of data at hand many models were developed to explain the traffic flow in various scenarios. However the possible ways of controlling the traffic behavior efficiently according to that knowledge have not been investigated extensively yet. This talk introduces two algorithms, which are widely used in communication networks, that possess properties which make them worthy candidates as control policies. I am going to investigate possible ways in which these methods, namely the Proportional Fair and the Backpressure Control, can be adapted for use in traffic control. I will discuss their advantages and disadvantages and present possible improvements and open questions in this field of research.
Madelon de Kemp - Robust appointment scheduling and sequencing for many patients
November 28, 2016
In this talk I will present the work I did for my master thesis. We consider the problem of scheduling appointments with a health care provider. We want to find schedules such that there is both little idle time between patients and little waiting time of patients. We will deal separately with the problem of determining the optimal time planned for each appointment, and of determining the optimal sequence. For both problems we will assume that we only know the mean and variance of the service times, and that the number of patients tends to infinity.
Maria Remerova - Queueing models with random fluid limits
November 21, 2016
Fluid limits of stochastic models are a law-of-large-numbers type of limit, and as such they are usually deterministic. In this talk I will present two queueing models that have random fluid limits: a polling model in overload and a model inspired by synchronization processes in the Bitcoin network.